四角錐體體積面積和體積 一 Dnfiyv
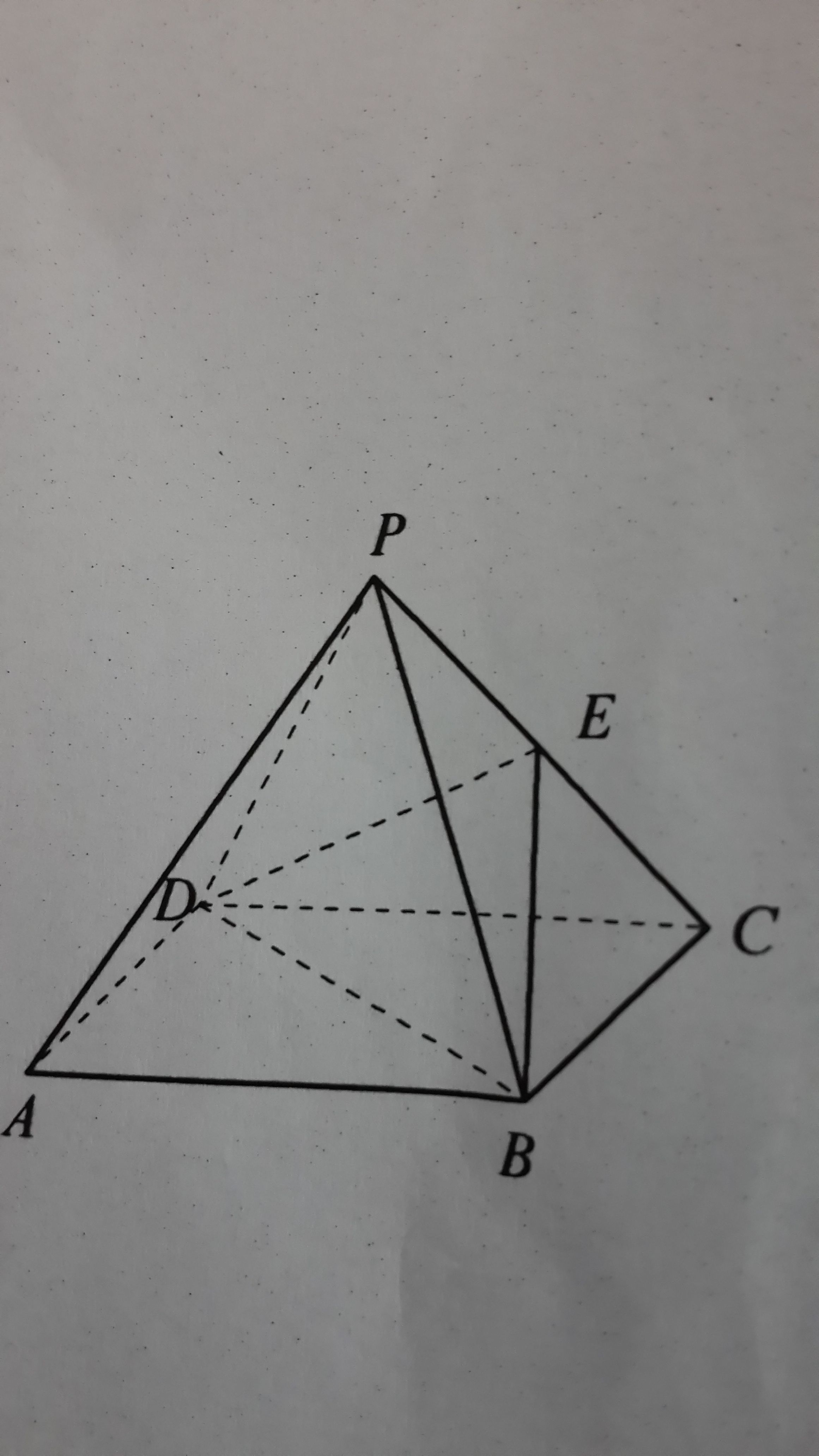
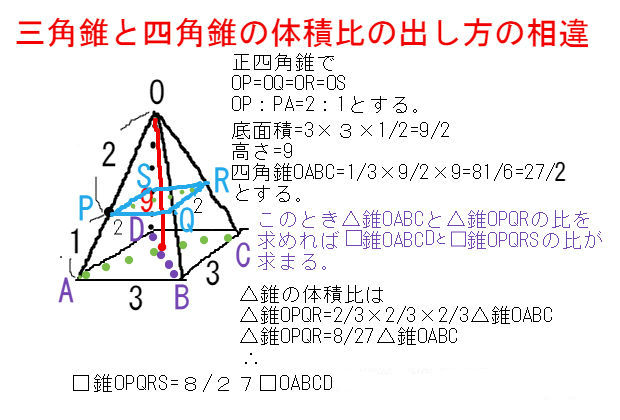
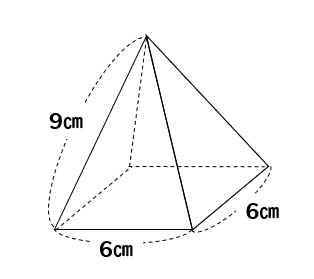
下図のような正四角錐oabcdがあり、その辺の長さはすべて6cmです。 oaを2：1に内分する点をpとします。 qはoc上を動きます。 平面bpqとodとの交点をrとします。 問題1 oq：qc=1：2の時、四角錐opbqrの体積を求めてください 問題2四角錐 長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab 、 体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は となる。 任意の正四角錐は、適当な 直交変換 により
正四角錐体積 公式
正四角錐体積 公式-図1．正四角錐の作り方 (2) 正四面体 この正四角錐には底がない。しかし、正四面体にすると、底ができる。 作り方（図2）：正四角錐の側面で、厚さが最も薄い側面に折り目を付ける（左図）。内側に折 り込んで、のりを付けて三角錐にする。 正四角錐の体積の求め方の公式って？？ こんにちは！この記事をかいているKenだよ。青い空が好きだね。 正四角錐の体積の求め方には公式があるんだ。 正四角錐って底面が正方形で、先がとんがっている立体のことだったよね。
正四稜錐 正四稜錐 底面是正方形 側面為4個全等的等腰三角形且有公共頂點 百科知識中文網
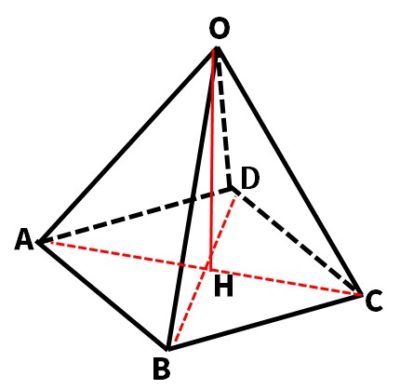
その他 棒折れ線円レーダーピラミッド等高線 正四面体の辺の長さ ホーム 数学公式集 体積・表面積正四面体の体積から辺の長さと表面積を計算します。 normalsize Regular tetrahedron volume hspace 50px large frac sqrt surface area hspace 10px sqrt お客様の声アンケート投稿よくある質問リンク方法正四面体の辺の長 こんにちは。相城です。今回は球の体積の何で？にお答えできればと存じます。 球の体積の公式のなぜ？ 球の中心を とし、頂点を とする正四角錐で球を 等分していくことを考える。 このとき、 を無限に近づけていくと、四角錐の高さは球の半径 に限りなく等しくなる。＜公式＞ 図のように正四角錐OABCDがあり、P,Q,R,Sを通る平面で切断したとします。 O P = a, O Q = b, O R = c, O S = d とすると、 1 a 1 c = 1 b 1 d という式が成り立ちます。 証明のようなもの ではそれの証明です。 東大の加法定理の証明問題、西大和高校の三平方の定理の証明問題みたいに公式の証明問題もたまに出ますし、やはり公式の証明はちゃんと知っておくべきだと僕は思います。
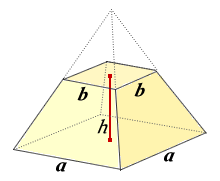
台形の体積（正四角錐台）の求め方の公式！ ？ 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、 {（下の辺）×（下の辺） （下の辺）×（上の辺） (上の辺) × (上の辺) }×高さ÷3 ってことさ。 たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体AC2= AC2=2 AC=±122 AC>0より AC=122 OからACに引いた垂線をOMとすると これが四角錐の高さになる。 AMはACの 1 2 なので AM=62 ≫ OAMで三平方の定理を使うと 152 =OM2 (62)2 OM2= OM2=153 OM=±317 OM>0よりOM=317 よって、高さ317, 底面積12×12=144 体積 144×317÷3=cm3 ≫類題練習 特別な直角三角形 三平方 折り返し 三平方の定理 pcスマホ問題 辺の長さが全て4である正四角錐がある。P、Qは中点である。このとき、四角錐OーAPQDの体積を求めよ。なんかいい方法ないですか？解説が複雑で・・・・問題わかりにくかったら行って下さい。 ① BODで四角睡を切断する。②三角錐ABODと三角錐APODについて、体積比は2：1になる。（∵ BODと PODを
正四角錐体積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 四面體 維基百科 自由的百科全書 | 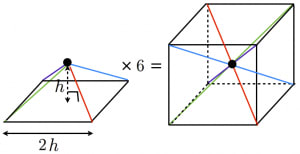 四面體 維基百科 自由的百科全書 | 四面體 維基百科 自由的百科全書 |
四面體 維基百科 自由的百科全書 | 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
四面體 維基百科 自由的百科全書 | 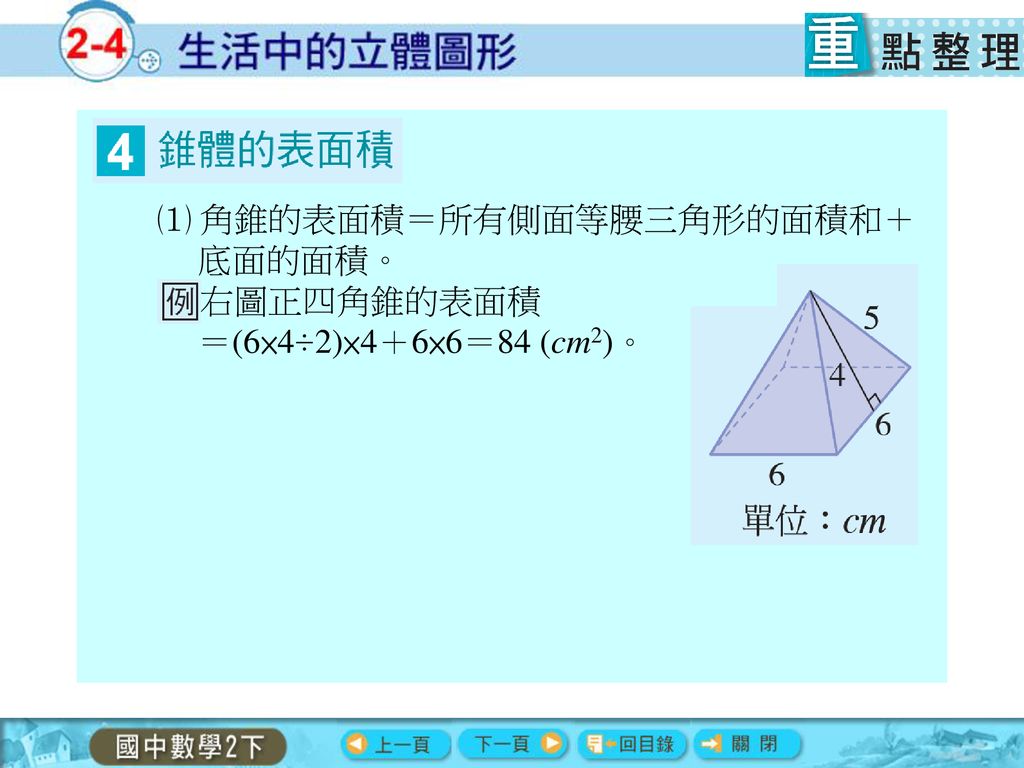 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
「正四角錐体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四面體 維基百科 自由的百科全書 | 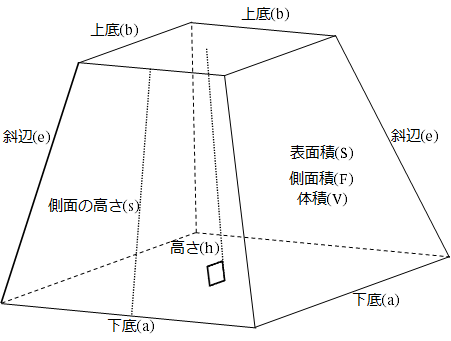 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 | 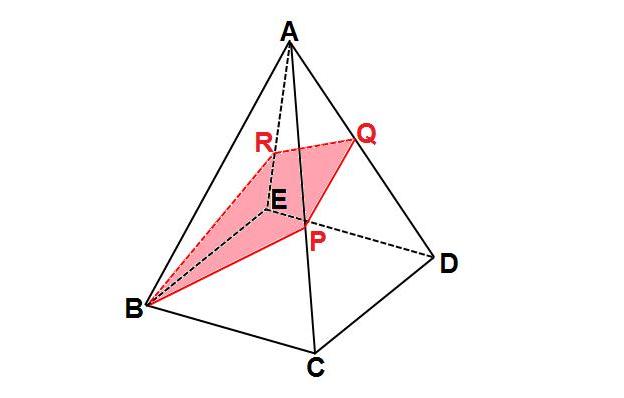 四面體 維基百科 自由的百科全書 | 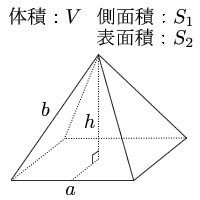 四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 | 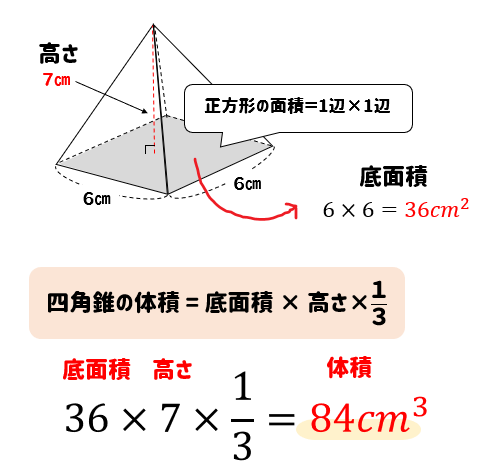 四面體 維基百科 自由的百科全書 |
「正四角錐体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 | 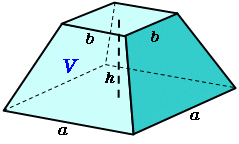 四面體 維基百科 自由的百科全書 |
「正四角錐体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 | 四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 | 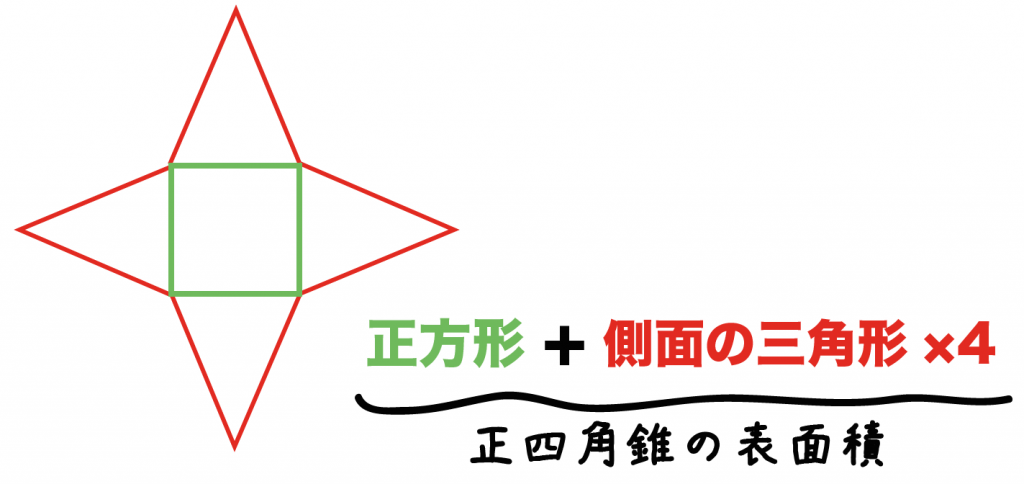 四面體 維基百科 自由的百科全書 | 四面體 維基百科 自由的百科全書 |
「正四角錐体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 | 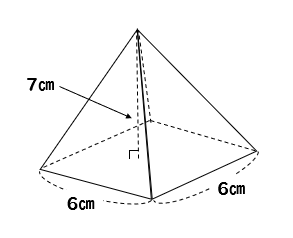 四面體 維基百科 自由的百科全書 |
四面體 維基百科 自由的百科全書 | 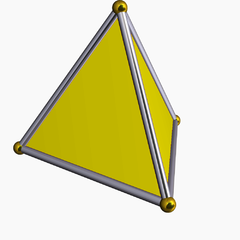 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 | 四面體 維基百科 自由的百科全書 |
「正四角錐体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
「正四角錐体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
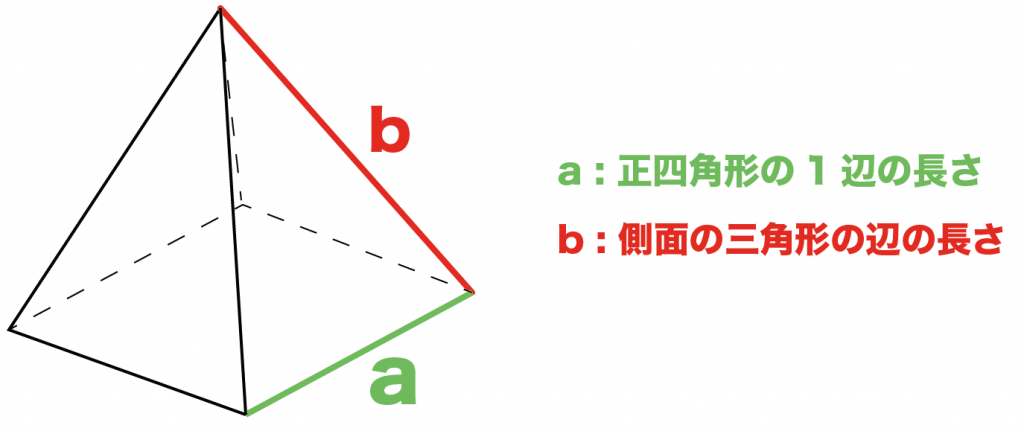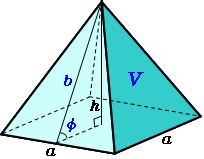 四面體 維基百科 自由的百科全書 | 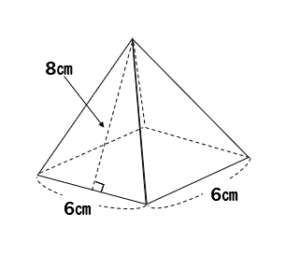 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |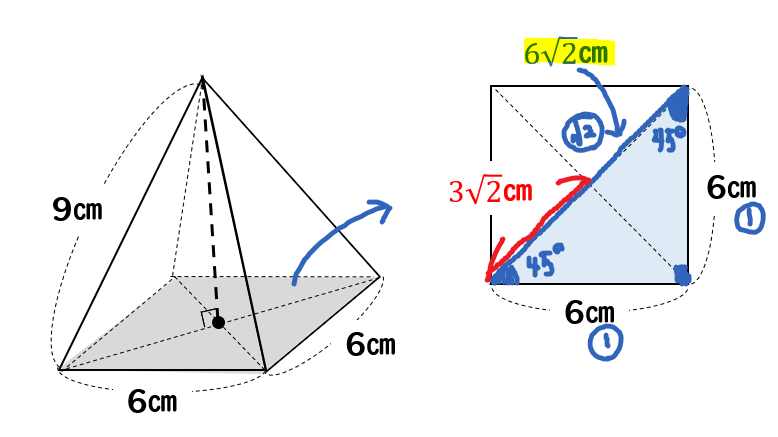
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
「正四角錐体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 | 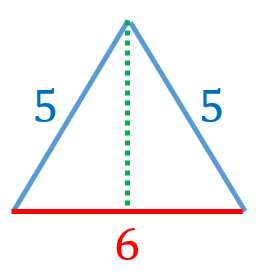 四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 | 四面體 維基百科 自由的百科全書 |
「正四角錐体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四面體 維基百科 自由的百科全書 | 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
「正四角錐体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四面體 維基百科 自由的百科全書 | 四面體 維基百科 自由的百科全書 | 四面體 維基百科 自由的百科全書 |
四面體 維基百科 自由的百科全書 | 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 | 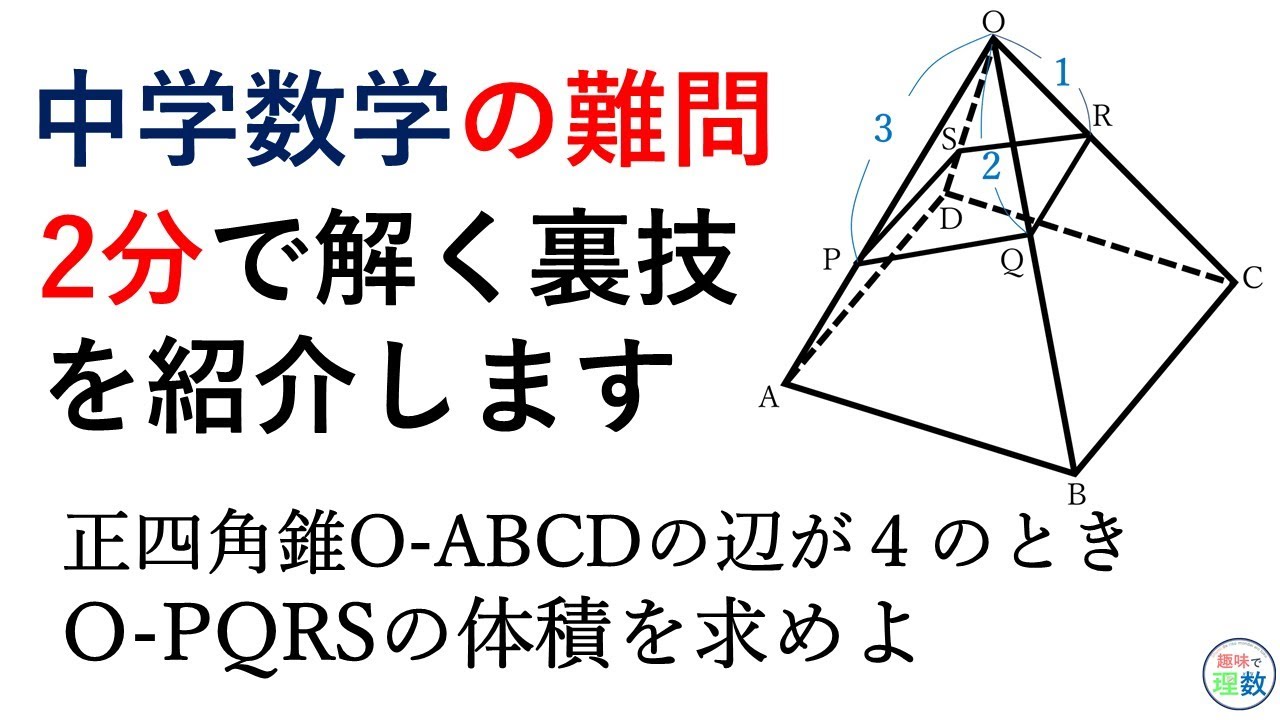 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
「正四角錐体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 | 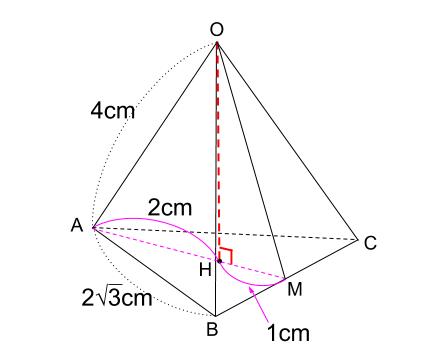 四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 | 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
「正四角錐体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四面體 維基百科 自由的百科全書 | 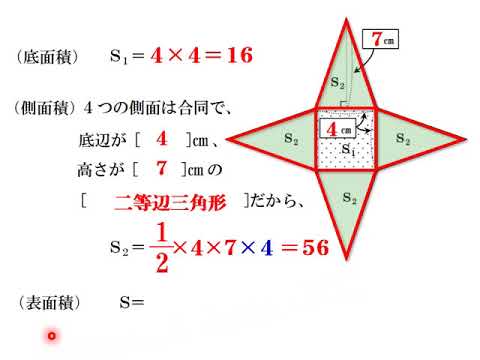 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
 四面體 維基百科 自由的百科全書 |  四面體 維基百科 自由的百科全書 |
※正四面体を正四角錐と書いてある間違いに2年くらい気づきませんでした。何してんだ。 中学生でも難なく解ける，正四面体の体積問題です。確か教員採用試験の問題集に載っていた。 「正四面体の体積と比率」 出典：オリジナル 中1数学、体積の問題 底面の一辺の長さがacm、高さがhcmの正四角錐がある。 ①この正四角錐の体積をV㎝3とするとき、Vをあ、hを使った式で求めなさい。 ②正四角錐の底面の1辺を3倍にし、高さを半分にすると、体積は何倍になりますか。
Incoming Term: 正四角錐体積 公式, 正四 角錐 中点 体積,
0 件のコメント:
コメントを投稿